On Drew's Day, February 12, 2010...
On Drew's Day, February 09, 2010...
How powerful is a physics professor, anyway?
Over at Dot Physics, Rhett has been explaining the inaccurate calculation of power on a TV show that I have never heard of or had the chance to see. He posted a video of himself pulling the family minivan with the family inside. He even posted a video of his 6-year old pulling the vehicle!
I assume that in a future post, he'll be giving the right way to calculate the power, but I couldn't resist trying out video analysis in Logger Pro with his video.
I analyzed the first 3.5 seconds after the van starts to move by clicking on the same point on the van every few frames. I used the wheel base of the 2007 Mazda 5 as a guess for the scale calibration.
I was pretty surprised that on my first attempt, the position-time data had a nice parabolic shape. I could have probably spent a little more time making sure that I always clicked on the exact same spot on the van, but for quick and dirty analysis, I'm pretty happy. Logger Pro defaults to motion to the left as having negative velocity. I didn't really try to reset this, as I only care about the magnitude of the rate of velocity change (i.e. the acceleration).
The acceleration is the slope of the velocity-time graph, so let's look at that:
So, using Rhett's free body diagram, we can apply Newton's second law:
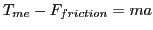 |
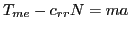 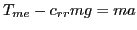 |
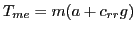 |
I googled around a bit and found that a typical auto on concrete has a coefficient of rolling resistance between 0.010 and 0.015, so I ballparked it at 0.012. Rhett gave the mass of the car in pounds, so I converted to kilograms.
Finally:
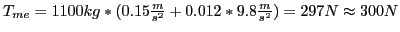 |
So the work done by our professor is equal to the force applied (300 N) multiplied by the distance through which the force acted (4.57 m). His power output during the pull is the work done divided by the time:
300 N * 4.57 m / 7.8 s = 176 W
That's a mighty bright light bulb, but it's just under twice the power radiated (on average) by a human that is just standing around doing nothing.
I know he was pulling at an angle, so his applied force is larger by the cosine of the angle, which I guesstimated to by 15 degrees, so make the applied force 310 N and the power 182 W if you want to be nitpicky about it...


